Have you ever wondered why radio waves seem to get weaker the further you get from the source of the waves? Well, they don't! They only appear to be weaker because they are spread over a larger area. This can be demonstrated by the inverse square law.
The inverse square law is a fundamental principle in physics that describes the relationship between the intensity of a phenomenon and the distance from its source. According to this law, the intensity of a phenomenon decreases in proportion to the square of the distance from its source. In other words, if you double the distance from the source, the intensity of the phenomenon decreases to one-fourth of its original value (i.e., 1/22); if you triple the distance, the intensity decreases to one-ninth of its original value (i.e., 1/32), and so on.
The inverse square law applies to many different phenomena, such as light, sound, gravity, and electromagnetic radiation (radio waves). For example, if you shine a flashlight in a dark room, the light will be brightest close to the flashlight and will become dimmer as you move farther away, following the inverse square law. Similarly, if you listen to a sound source, the sound will be loudest close to the source and will become quieter as you move farther away, also following the inverse square law.
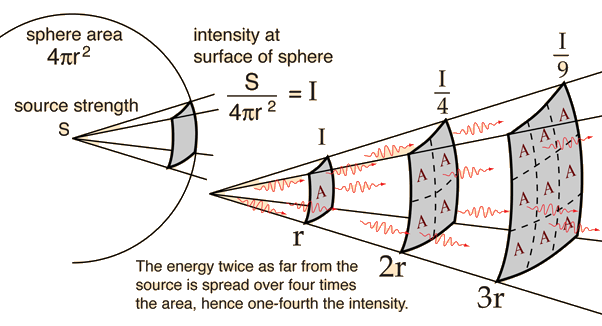
As radio waves travel through the air, they spread out and become weaker with increasing distance from the source. This means that the signal strength received by a receiver decreases with distance from the transmitter, and this effect is more pronounced the farther away the receiver is from the transmitter.
The inverse square law also affects the propagation of radio waves through obstacles and around corners. As radio waves encounter obstacles or are diffracted around corners, they spread out and become weaker in accordance with the inverse square law. This can cause problems with signal interference and attenuation, which can reduce the quality of the radio signal or even cause it to drop out entirely.
Ham radio operators can use the inverse square law to optimize their radio communications and to anticipate and mitigate signal attenuation and interference. Here are some ways in which the inverse square law can be useful for ham radio operators:
-
Estimating Signal Strength: The inverse square law can be used to estimate the signal strength of a radio transmission at a given distance from the transmitter. By measuring the signal strength at a known distance and applying the inverse square law, operators can estimate the signal strength at other distances, which can help them determine the optimal power output and antenna placement for their transmissions.
-
Antenna Placement: The inverse square law can also help ham radio operators determine the optimal placement of their antennas. The farther away the receiver is from the transmitter, the weaker the signal will be. By placing the antenna closer to the receiver, operators can minimize signal loss due to distance and maximize the signal-to-noise ratio.
-
Avoiding Interference: The inverse square law can also help ham radio operators avoid interference from other radio sources. Since the intensity of radio waves decreases with distance according to the inverse square law, operators can reduce the risk of interference by placing their antennas and receivers as far away as possible from other radio sources, such as power lines or other radio towers.
-
Predicting Propagation: The inverse square law can be used to predict the propagation of radio waves through the atmosphere. By modeling the effects of atmospheric conditions and terrain on radio wave propagation, operators can determine the best frequencies and power levels to use for their transmissions, as well as anticipate areas of poor signal quality due to terrain or atmospheric conditions.
Overall, understanding the inverse square law can help ham radio operators optimize their radio communications, avoid interference, and achieve better signal quality, which can be essential in emergency situations or in communicating over long distances.
